1、平衡二叉树定义:
平衡二叉树(Balanced Binary Tree或Height-Balanced Tree)又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。若将二叉树上结点的平衡因子bf(balance factor)定义为该结点的左子树的深度减去右子树的深度,则平衡二叉树上所有结点的平衡因子只可能为-1、0和1这三个值。
2、失去平衡情况分析:
假设结点A是一颗子平衡二叉树,当在以A为根结点的AVL树上插入一个新结点时,会出现以下三种情况:
1)如果插入前A?bf=1(A的左子树深度比右子树深度多1),如果插入在A的左子树上且A的左子树深度增加了1,则此时A?bf=2需要对树进行调整,如图2.1结点C为新插入的结点,C可以插入到B的左子树上(如图2.1(b))或者右子树上(如图2.1(c))。
2)如果插入前A?bf=0(A的左子树和右子树深度相等),如果插入在A的左子树上且A的左子树深度增加了1,则此时只需要改变A的平衡因子为1即可不需要对树进行调整。如果插入在A的右子树上且A的右子树深度增加了1,则此时只需要改变A的平衡因子为-1即可不需要进行调整。
3)如果插入前A?bf=-1(A的左子树深度比右子树深度少1),如果插入在A的右子树上且A的右子树深度增加了1,则此时A?bf=-2需要对树进行调整,如图2.2结点C为新插入的结点,C可以插入在B的左子树上(如图2.2(b))或者右子树上(如图2.2(c))。
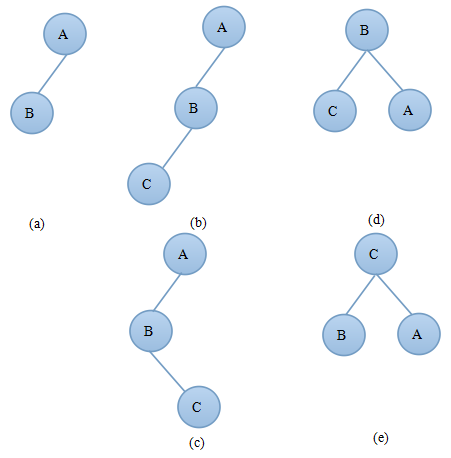
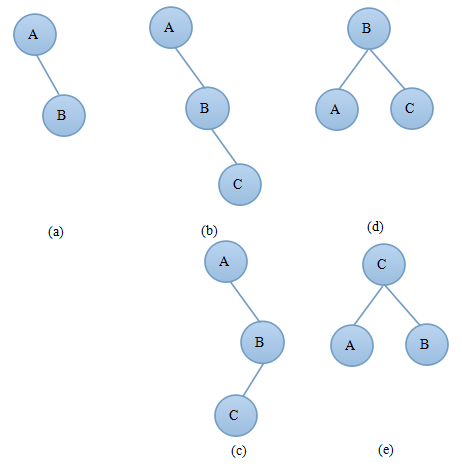
图2.1 图2.2
注意:上图中为了清楚的看到添加结点后失去平衡时的情况,省去了一些子结点,这些结点在下面的分析中会完整画出来
当出现图2.1(b)中的情况时只需要进行一次右旋转操作,旋转后得到如图2.1(d)所示的平衡二叉树。
当出现图2.1(c)中的情况时需要先对A的左子树B进行左旋操作,然后再进行右旋操作,旋转后得到如图2.1(e)所示的平衡二叉树。
当出现图2.2(b)中的情况时只需要进行一次右旋转操作,旋转后得到如图2.1(d)所示的平衡二叉树。
当出现图2.2(c)中的情况时需要先对A的右子树B进行右旋,然后再进行左旋操作,旋转后得到如图2.2(e)所示的平衡二叉树。
3.求旋转后各结点的平衡因子:
旋转后怎么确定各结点的新的平衡因子是平衡二叉树算法的关键点,我们需要按情况来一一推理。
一、当出现图2.1(b)(c)这两种情况时,需进行左平衡处理:
1)当新结点插入到B的左子树上时B?bf=1,由此可知:deep(C)=deep(E)+1,deep(B)=deep(C)+1;由于插入新结点前A?bf=1,deep(B)=deep(D)+1则插入新节点后deep(B)=deep(D)+2;图3.1.1为调整前的二叉树,图3.1.2为对A树进行右旋转后的AVL树:

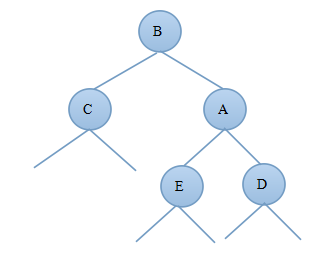
图3.1.1 图3.1.2
对比图3.1.1和3.1.2可知旋转后的新树中A的左子树发生了变化,B的右子树发生了变化,其他结点都没变;因此只需要重新算出A的平衡因子和B的平衡因子即可证明调整后的树是否为AVL树。
由上面的等式deep(B)=deep(D)+2,deep(B)=deep(C)+1,deep(C)=deep(E)+1
可以推出deep(E)=deep(C)-1=deep(B)-1-1=deep(D)+2-1-1=deep(D)可得出A?bf=0
由调整后deep(E)=deep(D)可推出调整后deep(A)=deep(E)+1=deep(C)-1+1=deep(C)可得出B?bf=0;
2)当新结点插入到B的右子树上时B?bf=-1,由此可知:deep(C)=deep(E)-1,deep(B)=deep(E)+1;由于插入新结点前A?bf=1,deep(B)=deep(D)+1则插入新节点后deep(B)=deep(D)+2;图3.2.1为调整前的二叉树,图3.2.2为先对B树进行左旋然后对A树进行右旋后的AVL树:
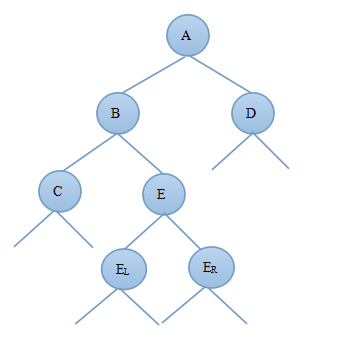
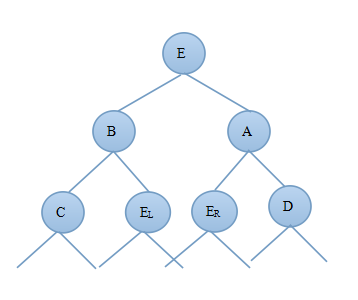
图3.2.1 图3.2.2
对比图3.2.1和3.2.2可知调整后的新树中A的左子树发生了变化,B的右子树发生了变化,E的左右子树都发生了变化,其他结点都没变,因此只需要重新算出A的平衡因子、B的平衡因子以及E的平衡因子即可证明调整后的树是否为AVL树。
此时由于调整后的B和A结点的平衡因子与E的左右子树EL和ER有关,因此需要根据E的平衡因子的不同来进行分析:
由上面的分析可得到deep(B)=deep(D)+2,deep(B)=deep(E)+1,deep(C)=deep(E)-1
1、当E?bf=1时:deep(E)=deep(EL)+1,deep(ER)=deep(EL)-1
deep(C)=deep(E)-1=deep(EL)+1-1=deep(EL)可得B?bf=0
deep(D)=deep(B)-2=deep(E)+1-2=deep(ER)+1+1+1-2=deep(ER)+1可得A?bf=-1
由于deep(EL)=deep(ER)+1所以E?bf=0
2、当E?bf=0时:deep(E)=deep(EL)+1,deep(ER)=deep(EL)
deep(C)=deep(E)-1=deep(EL)+1-1=deep(EL)可得B?bf=0
deep(D)=deep(B)-2=deep(E)+1-2=deep(ER)+1+1-2=deep(ER)可得A?bf=0
由于B?bf=0,A?bf=0所以E?bf=0
3、当E?bf=-1时:deep(E)=deep(ER)+1,deep(ER)=deep(EL)+1
deep(C)=deep(E)-1=deep(EL)+1+1-1=deep(EL)+1可得B?bf=1
deep(D)=deep(B)-2=deep(E)+1-2=deep(ER)+1+1-2=deep(ER)可得A?bf=0
由于deep(EL)=deep(ER)-1所以E?bf=0
二、当出现图2.2(b)(c)这两种情况时,需进行右平衡处理:
1)当新结点插入到C的左子树上时C?bf=1,由此可知:deep(C)=deep(E)+1,deep(D)=deep(E)-1;由于插入新结点前A?bf=-1,deep(B)=deep(C)-1则插入新节点后deep(B)=deep(C)-2;图3.3.1为调整前的二叉树,图3.3.2为先对C树进行右旋然后对A树进行左旋后的AVL树:
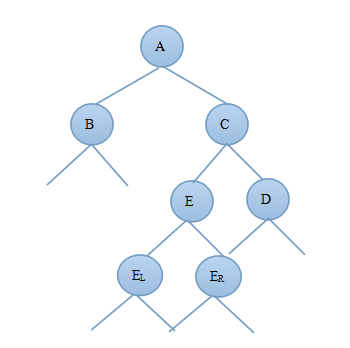
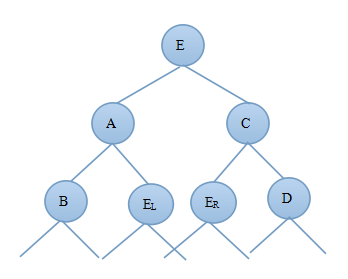
图3.3.1 图3.3.2
对比图3.3.1和3.3.2可知调整后的新树中A的右子树发生了变化,C的左子树发生了变化,E的左右子树都发生了变化,其他结点都没变,因此只需要重新算出A的平衡因子、B的平衡因子以及E的平衡因子即可证明调整后的树是否为AVL树。
此时由于调整后的A和C结点的平衡因子与E的左右子树EL和ER有关,因此需要根据E的平衡因子的不同来进行分析:
由上面的分析可得到deep(B)=deep(C)-2,deep(C)=deep(E)+1,deep(D)=deep(E)-1
1、当E?bf=1时:deep(E)=deep(EL)+1,deep(ER)=deep(EL)-1
deep(B)=deep(C)-2=deep(EL)+1+1-2=deep(EL)可得A?bf=0
deep(D)=deep(E)-1=deep(ER)+1+1-1=deep(ER)+1可得C?bf=-1
由于deep(EL)=deep(ER)+1所以E?bf=0
2、当E?bf=0时:deep(E)=deep(EL)+1,deep(ER)=deep(EL)
deep(B)=deep(E)+1-2=deep(EL)+1+1-2=deep(EL)可得A?bf=0
deep(D)=deep(E)-1=deep(ER)+1-1=deep(ER)可得C?bf=0
由于A?bf=0,C?bf=0所以E?bf=0
3、当E?bf=-1时:deep(E)=deep(ER)+1,deep(ER)=deep(EL)+1
deep(B)=deep(C)-2=deep(E)+1-2=deep(EL)+1+1+1-2=deep(EL)+1可得A?bf=1
deep(D)=deep(E)-1=deep(ER)+1-1=deep(ER)可得C?bf=0
由于deep(EL)=deep(ER)-1所以E?bf=0
2)当新结点插入到C的右子树上时C?bf=-1,由此可知:deep(C)=deep(D)+1,deep(D)=deep(E)+1;由于插入新结点前A?bf=-1,deep(B)=deep(C)-1则插入新节点后deep(B)=deep(C)-2;图3.4.1为调整前的二叉树,图3.4.2为进行左旋后的AVL树:
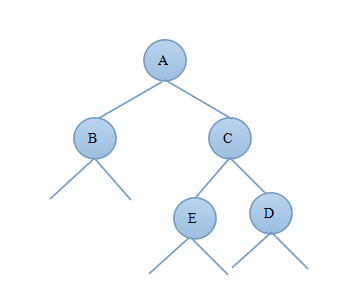
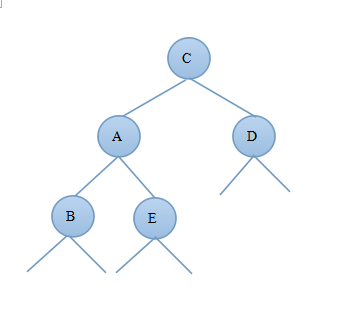
图3.4.1 图3.4.2
对比图3.4.1和3.4.2可知调整后的新树中A的右子树发生了变化,C的左子树发生了变化,其他结点都没变,因此只需要重新算出A的平衡因子和C的平衡因子即可证明调整后的树是否为AVL树。
由上面的等式deep(B)=deep(C)-2,deep(C)=deep(D)+1,deep(D)=deep(E)+1
可以推出deep(B)=deep(C)-2=deep(D)+1-2=deep(E)+1+1-2=deep(E)可得出A?bf=0
由A?bf=0调整后deep(A)=deep(E)+1=deep(D)-1+1=deep(D)可得出C?bf=0;
4.Java实现代码:
package org.algorithms.tree;
import java.util.concurrent.ConcurrentLinkedQueue;
public class BalanceBiTreeT {
private Node root;
private int size;
public void insert(T t){
if(root==null){
root = new Node();
root.bf = 0;
root.data = t;
size++;
return;
}
addNode(root,t);
}
private boolean addNode(Node nd,T t){
boolean taller = false;
ComparableT cp = (ComparableT)nd.data;
int i = cp.compareTo(t);
if(i==0){
return false;
}else if(i0){
if(nd.lChild==null){
Node child = new Node();
child.bf = 0;
child.data = t;
child.parent = nd;
nd.lChild = child;
size++;
if(nd.bf==0){
nd.bf = 1;
return true;
}
nd.bf = 0;
}else{
taller = addNode(nd.lChild, t);
if(taller){
if(nd.bf==1){
leftBalance(nd);
taller = false;
}else if(nd.bf==0){
nd.bf = 1;
taller = true;
}else{
nd.bf = 0;
taller = false;
}
}
}
}else{
if(nd.rChild==null){
Node child = new Node();
child.bf = 0;
child.data = t;
child.parent = nd;
nd.rChild = child;
size++;
if(nd.bf==0){
nd.bf = -1;
return true;
}
nd.bf = 0;
}else{
taller = addNode(nd.rChild, t);
if(taller){
if(nd.bf==1){
nd.bf = 0;
taller = false;
}else if(nd.bf==0){
nd.bf = -1;
taller = true;
}else{
rightBalance(nd);
taller = false;
}
}
}
}
return taller;
}
public int getSize(){
return size;
}
private void leftBalance(Node nd){
Node leftChild = nd.lChild;
if(leftChild.bf==1){
nd.bf = 0;
leftChild.bf = 0;
rightRotate(nd);
}else if(leftChild.bf==-1){
Node rd = leftChild.rChild;
switch (rd.bf) {
case 1:
leftChild.bf=0;nd.bf = -1;
break;
case 0:
leftChild.bf=0;nd.bf = 0;
break;
case -1:
leftChild.bf = 1;nd.bf = 0;
break;
}
rd.bf = 0 ;
leftRotate(leftChild);
rightRotate(nd);
}
}
private void rightBalance(Node nd){
Node rightChild = nd.rChild;
if(rightChild.bf==1){
Node ld = rightChild.lChild;
switch (ld.bf) {
case 1:
rightChild.bf= -1; nd.bf = 0;
break;
case 0:
rightChild.bf=0;nd.bf = 0;
break;
case -1:
rightChild.bf = 0;nd.bf = 1;
break;
}
ld.bf = 0 ;
rightRotate(rightChild);
leftRotate(nd);
}else if(rightChild.bf==-1){
nd.bf = 0;
rightChild.bf = 0;
leftRotate(nd);
}
}
private void leftRotate(Node nd){
Node top = nd.rChild;
nd.rChild = top.lChild;
if(top.lChild!=null)
top.lChild.parent = nd;
top.lChild = nd;
top.parent = nd.parent;
if(nd.parent!=null){
if(nd.parent.lChild == nd)
nd.parent.lChild = top;
else
nd.parent.rChild = top;
}else{
root = top;
}
nd.parent = top;
}
private void rightRotate(Node nd){
Node top = nd.lChild;
nd.lChild = top.rChild;
if(top.rChild!=null)
top.rChild.parent = nd;
top.rChild = nd;
top.parent = nd.parent;
if(nd.parent!=null){
if(nd.parent.lChild == nd)
nd.parent.lChild = top;
else
nd.parent.rChild = top;
}else{
root = top;
}
nd.parent = top;
}
public void printTree(){
ConcurrentLinkedQueueNode queue = new ConcurrentLinkedQueueNode();
ConcurrentLinkedQueueNode tempQueue = new ConcurrentLinkedQueueNode();
queue.add(root);
int offset= 0;
int counter=2;
for(int i=0;i50;i++)
System.out.print(" ");
while(queue.peek()!=null){
Node node = queue.poll();
String side = "L";
if(node.parent!=nullnode.parent.rChild==node)
side = "R";
System.out.print(node.data+"("+(node.parent==null?"":node.parent.data)+" "+side+")");
if(node.parent!=nullnode.parent.rChild!=node)
for(int i=0;icounter;i++)
System.out.print(" ");
if(node.lChild!=null)
tempQueue.add(node.lChild);
if(node.rChild!=null)
tempQueue.add(node.rChild);
if(queue.isEmpty()){
offset += 3;
//counter--;
copyQueue(tempQueue,queue);
System.out.println();
for(int i=0;i50-offset;i++)
System.out.print(" ");
}
}
}
private void copyQueue(ConcurrentLinkedQueueNode source,
ConcurrentLinkedQueueNode target){
while(source.peek()!=null){
target.add(source.poll());
}
}
private class Node{
public T data;
public Node lChild;
public Node rChild;
public Node parent;
public int bf;
}
}