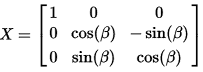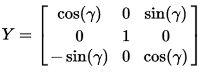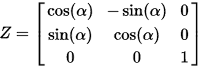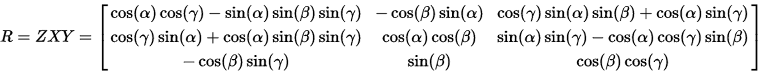神奇的第三维度 | 少将全栈

很多技术同学都是游戏玩家，3D游戏无疑是画面最棒、投入感最真实、最让人投入的。

说起3D，前端工程师们应该都很熟悉，CSS3对3D支持非常好，除部分低端Android机器外，性能和效果都不错。今天来分享下如何基于HTML5陀螺仪，来实现3D虚拟现实效果。

移动端虚拟现实

虚拟现实大家肯定都了解。VR视觉增强的电影、游戏，市面上已经有很多了。

我们这里的VR，就是简单的用手机屏幕来当虚拟摄像机，让你来“观察”四周，感觉仿佛置身于虚拟环境里。我们团队有两个互动应用

星辰大海：http://www.tmall.com/go/chn/common/tgp-startui.php (把活动取消的提示叉掉就行:) )

，

汽车内景: http://m.laiwang.com/market/laiwang/tmall-vr-car.php?carid=2

这是天猫互动在 “陀螺仪感应” 结合 “虚拟3D技术” 的一次尝试，事实证明在某些特定商品(比如汽车)上效果非常好。

如果你看完Demo很感兴趣，那接下来让我一步一步分解这里面涉及到的所有内容。

矩阵

计算机3D图形和矩阵密切相关，图形API接口也都直接使用矩阵，下面简单列举下矩阵一些简单概念

CSS3 transform

Transform2d/3d 封装了最基本的变换操作。每个变换都可以转化为矩阵。我们只说虚拟现实涉及的几个3D变换

rotateX()
rotateY()
rotateZ()
scale3d(sx, sy, sz)

以上都是正交矩阵，简单说就是坐标系原点不变。

translate3d 使坐标原点变换，因此使用“仿射矩阵”来描述
rotate3d(x, y, z, a) 这个比较特殊，描述的不是矩阵，而是“四元数”

详细信息可查看https://developer.mozilla.org/en-US/docs/Web/CSS/transform-function

以汽车内景Demo为例，旋转+透视点距离，使用了rotate+translateZ，手指缩放使用了scale3d。

矩阵不满足乘法交互率

多个矩阵变换叠加起来，就是是矩阵相乘。一个很重要的概念：矩阵不满足乘法交互率！这就意味着变换顺序的不同，直接导致最终结果千差万别。

通俗的讲就是：每一次变换都是相对上一次变换来做的，参考的坐标系时刻都在变化，无论2D、3D里都一样；

所以：translateZ() rotateX() rotateY() 和 rotateY() rotateX() translateZ() 得出的结果完全相反。

下一步我们要做的就是：如何将手机陀螺仪的数据正确反映出来！

陀螺仪

欧拉角

说陀螺仪之前，一定要先说这个概念欧拉角。欧拉角广泛应用于航空航天领域，当然还有我们最熟悉的手机陀螺仪方位感应器 deviceorientaiton

欧拉角描述3D空间里的方位，陀螺仪监听接口返回 alpha、beta、gamma 就是标准欧拉角方位。(这是手机端，欧拉角官方名称是 heading，pitch、bank)

两个不同的旋转顺序：(heading:45,bank:90) 和（bank:90,pitch:45）在效果是一致的，一个刚体的方位，可以表示成欧拉角多种不同的旋转顺序。也因为欧拉角的不唯一性，会产生“万向锁”的问题。

限制性欧拉角

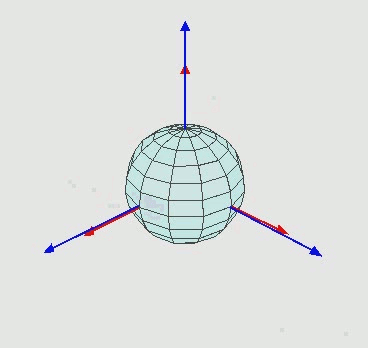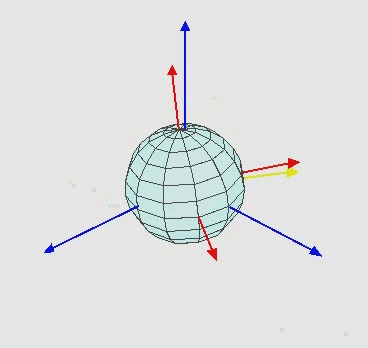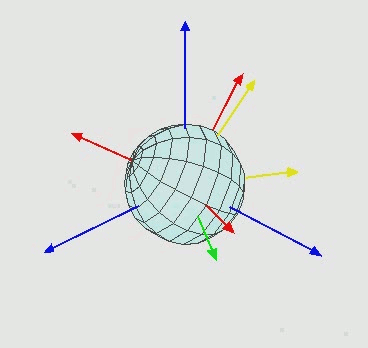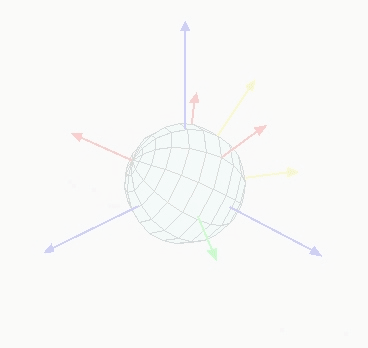
为了保证唯一性，就有了“限制性欧拉角”这个概念。任何一个方位的描述，是按 alpha, beta, gamma 顺序旋转来得出的方位角度的。可以看成三个旋转正交矩阵，顺序相乘得出变换后的坐标，看下面的动态图，来帮助理解

先绕蓝色Z轴旋转，得出alpha，然后绕绿色轴旋转，得出beta，最后绕红色轴旋转，得出gamma；

最后这张示意图一目了然：

限制性欧拉角有一些特性：

取值范围：alpha：0-360，beta：+-90，gamma：+-180
beta = +-90时，既手机翻转，alpha、gamma会瞬间 +-180；

欧拉角可参考这本书：3D数学基础:图形与游戏开发第十章

代码实现：

前面全是介绍概念，接下来才是正题。相信我，真正的代码远没有你想象中复杂。

现在我们已知了限制性欧拉角三个方位：alpha、beta、gamma，接下来的工作就是转换成矩阵，提供给你所使用的图像API。

我们使用 CSS3 rotate3d，来操作一个已建模的正立方体，关于如何使用DIV+ Perspective3d 来构建一个3D立方体，又是另外一个话题了，但其实也很简单。大家可以看上面汽车Demo的样式。相关内容会在下期“伪3D”专题中说明

alpha、beta、gamma 一一对应 rotateZ()、rotateX()、rotateY()，相对于我们的Z轴向上的世界坐标系而言。

所以欧拉角方位最终的矩阵变换公式是：

使用CSS3就意味着不用关心矩阵，除非你想用 matrix3d()。但矩阵相乘是顺序相关的，所以你必须关注每个变换的顺序。代码超简单就是这样…..

style.webkitTransform = [’rotateZ(Zdeg) ’,’rotateX(Xdeg) ’,’rotateY(Ydeg)’].join(’’);

最终的效果应该是，你所看的立方体相对于环境，位置是不变的。

发现不对？呵呵，没错，因为陀螺仪返回的是手机相对于世界坐标系的方位。

相对屏幕坐标系的逆矩阵

何为虚拟现实，就是你在屏幕中看到的物体，相对于环境是不动的，只是你的摄像机角度变了而已。而图形API所做的变换，都是相对手机屏幕的。下面是一段比较绕的逻辑：

陀螺仪的矩阵变换最终是 ZXY
相乘。这是相对世界坐标系，你的手机屏幕按照这个矩阵变换到现在的方位，但是屏幕中的物体，被施加的矩阵变换是相对屏幕坐标系的，为了让它相对于世界坐标
系保持不变。所以最终图形API所需要的矩阵变换，是ZXY相反的方向，也就是它的逆矩阵！

ZXY将顺序颠倒相乘，YXZ 就能得到相应的逆矩阵。所以！我们最终的代码应该是：

Style.webkitTransform = [’rotateY(Ydeg) ’, ’rotateX(Xdeg) ’, ’rotateZ(Zdeg)’].join(’’);

大功告成！

基于两轴的变换

Android同学可能发现上面的汽车Demo，只能用滑屏操作，因为大部分Android机器的陀螺仪非常不稳定+不精确，抱歉了！

手指滑动逻辑也很简单，因为只改变了两个轴的旋转，代码如下：

style.webkitTransform = ’rotateZ(0) rotateX(Xdeg) rotateY(Ydeg)’;

注意这里的变换顺序也是不能改的，不然直接影响到你的交互。然后给X轴角度做个+-90°的取值范围就能防止颠倒效果。

切换不同的图形API

如果你不使用CSS3，那这些矩阵计算都得自己代码实现。我们完全可以使用webGL来渲染整个立方体，除了图形API不同，webGL所需要的变换矩阵完全一致；

WebGL是不二的选择，而且可以构建更加复杂的球体来渲染全景，这时候素材就需要一张全景图片。不使用框架的话，会有点复杂，我们采用Three.js来构建我们的webGL版本

上代码：

新建一个球体 Geometry，使用Threejs.BackSide 内部渲染时，为了消除材质的镜像显示，要设置一个scaleX(-1)，也就是实现左右颠倒

var geometry = new THREE.SphereGeometry(perspective, 100, 100);
geometry.applyMatrix( new THREE.Matrix4().makeScale( -1, 1, 1 );

设置全景图素材

var material = new THREE.MeshBasicMaterial({
    map: texture,
    overdraw: 1,
    side: THREE.BackSide
});
var mesh = new THREE.Mesh(geometry, material);

箭头deviceorientation事件，构建Euler对象，因为Threejs是左手坐标系，和CSS3坐标系不同，所以Y、Z轴顺序需要颠倒

euler.set( beta * Degree, alpha * Degree, gamma * Degree,’YXZ’ );

Euler转换为四元数（quaternion）

camera.quaternion.setFromEuler( euler );

Three.js Demo, 滑轮/双指缩放可以更改摄像机FV

http://g.alicdn.com/tmapp/vr-car/1.1.1/demo/webgl.html

陀螺仪的其他应用

指南针：需要计算真实世界里手机头部的向量坐标，无需逆矩阵，ZXY即可，然后计算这个向量在水平面上的投影坐标；
游戏操控：
- 根据欧拉角来计算游戏中摄像机的角度变换，应用场景广泛；
- 根据设备方位 + socket即时通信，实现无线鼠标的效果；
虚拟重力：类似指南针原理，计算手机底部的向量坐标。可以结合物理引擎来做一些重力游戏；
方位手势：用户可获得左右翻转、上下翻转的手势体验；

总结

以上就是基于手机陀螺仪的虚拟现实原理。我数学功底不扎实，很多描述不是很详细，如果你还是不太理解，欢迎随时来讨论。

前端工程师作为一个产品中人机交互的第一道门槛，创造性的交互方式、富有画面感的效果，能起对产品起到很积极的作用。个人认为掌握前沿的图形显示技术，对产品体验、技能提升都有很大帮助的。

转自：https://github.com/tmallfe/tmallfe.github.io/issues/21