本章主要是Crazepony核心的算法讲解。其中最重要的就是姿态解算部分内容。
姿态解算是指把陀螺仪、加速度计、罗盘等数据融合在一起,得出飞行器的空中姿态,也叫做姿态融合。姿态解算的过程,涉及到传感器数据读取与滤波,四元数与旋转,姿态解算框架,长期融合/快速融合。
姿态解算的英文是attitude algorithm,也叫做姿态分析,姿态估计,姿态融合。姿态解算是指把陀螺仪、加速度计、罗盘等的数据融合在一起,得出飞行器的空中姿态。
飞行器从陀螺仪的三轴角速度通过四元数法得到的俯仰、偏航和滚转角,这是快速解算,结合三轴地磁和三轴加速度得到漂移补偿和深度解算。
数学模型
姿态是用来描述一个刚体的固连坐标系和参考坐标系之间的角位置关系,有一些数学表示方法。很常见的就是欧拉角,四元数,矩阵,轴角。
姿态解算需要解决的是四轴飞行器和地球的相对姿态问题。地球的坐标系又叫做地理坐标系,是固定不变的。正北,正东,正向上构成了这个坐标系的X,Y,Z轴,我们用坐标系R表示。四轴飞行器上固定着一个坐标系,用坐标系r表示。那么我们就可以用欧拉角,四元数等来描述r和R的角位置关系。这就是四轴飞行器姿态解算的数学模型和基础。

角位置关系测量
如上所说,地球坐标系R是固定的。四轴飞行器上固定一个坐标系r,这个坐标系r在坐标系R中运动。那么如何知道坐标系r和坐标系R的角位置关系呢,
也就是怎么知道飞行器相对于地球这个固定坐标系R转动了一下航向,或者侧翻了一下机身,或者掉头下栽。这就是传感器需要测量的数据,传感器包括陀螺仪,加
速度计,磁力计。通过获得这些测量数据,得到坐标系r和坐标系R的角位置关系,这就是姿态解算。
姿态的数学表示方法
姿态有多种数学表示方式,常见的是四元数,欧拉角,矩阵和轴角。他们各自有其自身的优点,在不同的领域使用不同的表示方式。在四轴飞行器中使用到了四元数和欧拉角。
四元数
四元数是由爱尔兰数学家威廉?卢云?哈密顿在1843年发现的数学概念。从明确地角度而言,四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话,四元数就代表着一个四维空间,相对于复数为二维空间。
四元数大量用于电脑绘图(及相关的图像分析)上表示三维物件的旋转及方位。四元数亦见于控制论、信号处理、姿态控制、物理和轨道力学,都是用来表示旋转和方位。
相对于另几种旋转表示法(矩阵,欧拉角,轴角),四元数具有某些方面的优势,如速度更快、提供平滑插值、有效避免万向锁问题、存储空间较小等等。
以上部分摘自维基百科-四元数。
欧拉角
莱昂哈德?欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。参考系又称为实验室参考系,是静止不动的。而坐标系则固定于刚体,随着刚体的旋转而旋转。
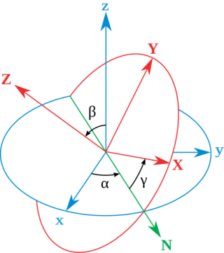
以上部分摘自维基百科-欧拉角。下面我们通过图例来看看欧拉角是如何产生的,并且分别对应哪个角度。
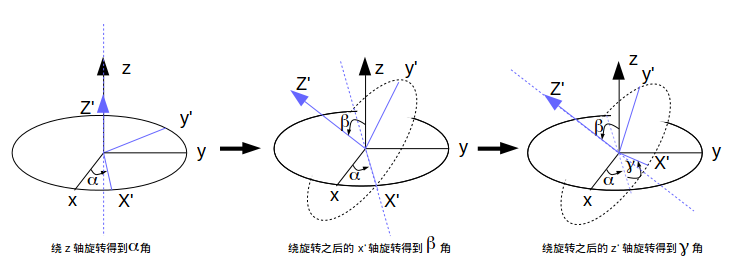
姿态解算为什么要用四元数和欧拉角
姿态解算的核心在于旋转,一般旋转有4种表示方式:矩阵表示、欧拉角表示、轴角表示和四元数表示。矩阵表示适合变换向量,欧拉角最直观,轴角表示则
适合几何推导,而在组合旋转方面,四元数表示最佳。因为姿态解算需要频繁组合旋转和用旋转变换向量,所以采用四元数保存组合姿态、辅以矩阵来变换向量的方
案。
总结来说,在crazepony中,姿态解算中使用四元数来保存飞行器的姿态,包括旋转和方位。在获得四元数之后,会将其转化为欧拉角,然后输入到姿态控制算法中。
姿态控制算法的输入参数必须要是欧拉角。AD值是指MPU6050的陀螺仪和加速度值,3个维度的陀螺仪值和3个维度的加速度值,每个值为16位精
度。AD值必须先转化为四元数,然后通过四元数转化为欧拉角。这个四元数可能是软解,主控芯片(STM32)读取到AD值,用软件从AD值算得,也可能是
通过MPU6050中的DMP硬解,主控芯片(STM32)直接读取到四元数。具体参考《MPU60x0的四元数生成方式介绍》。
下面就是四元数软解过程,可以由下面这个框图表示:
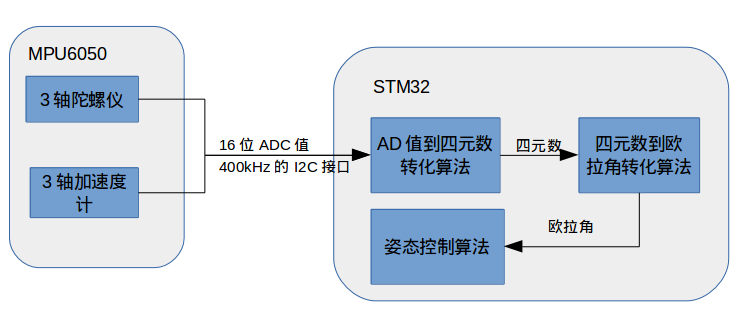
扩展阅读-四元数的运算
下面介绍一下四元数,然后给出几种旋转表示的转换。这些运算在crazepony的代码中都会遇到。
四元数可以理解为一个实数和一个向量的组合,也可以理解为四维的向量。这里用一个圈表示q是一个四元数(很可能不是规范的表示方式)。
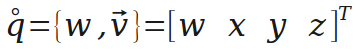
四元数的长度(模)与普通向量相似。
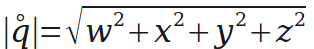
下面是对四元数的单位化,单位化的四元数可以表示一个旋转。
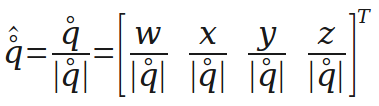
四元数相乘,旋转的组合就靠它了。
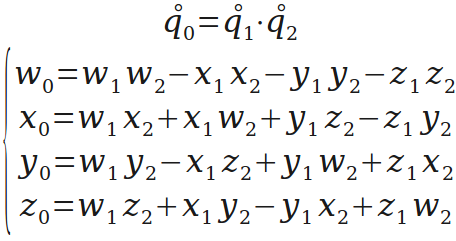
旋转的“轴角表示”转“四元数表示”。这里创造一个运算q(w,θ),用于把绕单位向量w转θ角的旋转表示为四元数。
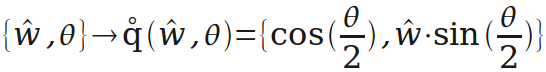
通过q(w,θ),引伸出一个更方便的运算q(f,t)。有时需要把向量f的方向转到向量t的方向,这个运算就是生成表示对应旋转的四元数的(后面会用到)。
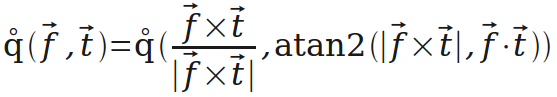
然后是“四元数表示”转“矩阵表示”。再次创造运算,用R(q)表示四元数q对应的矩阵(后面用到)。
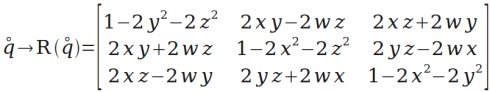
多个旋转的组合可以用四元数的乘法来实现。
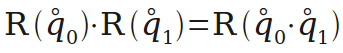
“四元数表示”转“欧拉角表示”。用于显示。

陀螺仪
陀螺仪,测量角速度,具有高动态特性,但是它是一个间接测量角度的器件,它测量的是角度的导数,角速度,要将角速度对时间积分才能得到角度。
如果这个世界是理想的,美好的,那我们的问题到此就解决了,不过很遗憾,现实是残酷的,误差的引入,使得积分出现了问题。
假设陀螺仪固定不动,理想角速度值是0dps(degree per
second),但是有一个偏置0.1dps加在上面,于是测量出来是0.1dps,积分一秒之后,得到的角度是0.1度,1分钟之后是6度,还能忍受,
一小时之后是360度,转了一圈,也就是说,陀螺仪在短时间内有很大的参考价值。
使用陀螺仪获得角度,一定要考虑积分误差的问题。
加速度计
加速度计可以测量加速度,包括重力加速度,于是在静止或匀速运动的时候,加速度计仅仅测量的是重力加速度,而重力加速度与刚才所说的R坐标系是固连的,通过这种关系,可以得到加速度计所在平面 与 地面 的角度关系.
但是加速度计若是绕着重力加速度的轴转动,则测量值不会改变,也就是说无法感知这种水平旋转。
MPU6050姿态测量的两种方法
MPU-60×0是9轴运动处理传感器。它集成了3轴MEMS陀螺仪,3轴MEMS加速度计,以及一个可扩展的数字运动处理器
DMP(Digital Motion
Processor),可用I2C接口连接一个第三方的数字传感器,比如磁力计。扩展之后就可以通过其I2C或SPI接口输出一个9轴的信号。
MPU-60×0对陀螺仪和加速度计分别用了三个16位的ADC,将其测量的模拟量转化为可输出的数字量。在Crazepony-II上,测试了软
件解算四元数,然后通过四元数解算姿态角这种实现方式,其实总的来说,并没感觉36MHz的主控压力有多大,没有出现机身不稳,卡死的情况。

同时,本着务实的态度,我们也测试了MPU6050的硬解四元数,即从IIC总线上读到的数据不再是MPU60x0的AD值,而是通过初始化对
DMP引擎的配置,从IIC总线上读到的直接就是四元数的值,从而跳过了程序通过AD值计算四元数这个看起来繁琐的步骤。测试结果是,机身反应的确要比之
前反应灵活,最关键的一点是,这样得出的偏航角(Yaw)很稳很稳,基本不会漂移或者说漂移小到了可以容忍的地步。
最后,MPU60x0的强大之处不仅于此,它支持一个从IIC接口,可以外部接上一个磁力计,如HMC5883,这样一来,DMP引擎可以直接输出
一个绝对的方向姿态,即能够输出一个带东西南北的姿态数据包,很厉害的样子。在Crazepony-II第四版将会加上这样一个磁力计,相信它再也不会迷
路了~~
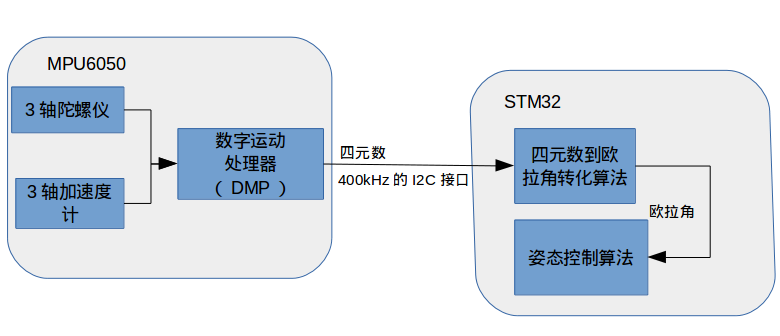
姿态解算流程图
快速融合
长期融合
秦永元《惯性导航》
袁信、郑锷的《捷联式惯性导航原理》,邓正隆的《惯性技术》
软件姿态解算
文中有很多word下编辑的公式尚未加入,需要继续完善
使用MPU6050硬件DMP解算姿态是非常简单的,下面介绍由三轴陀螺仪和加速度计的值来使用四元数软件解算姿态的方法。
我们先来看看如何用欧拉角描述一次平面旋转(坐标变换):
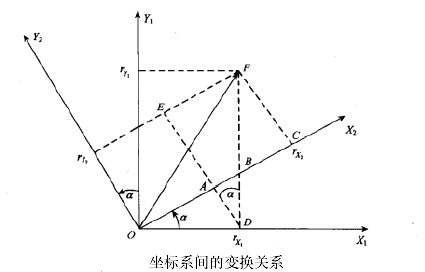
设坐标系绕旋转α角后得到坐标系,在空间中有一个矢量在坐标系中的投影为,在内的投影为由于旋转绕进行,所以Z坐标未变,即有。
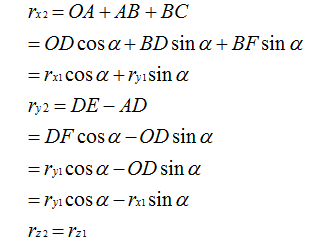
转换成矩阵形式表示为:
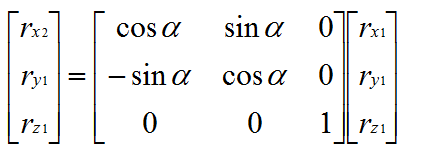
整理一下:

所以从旋转到可以写成
上面仅仅是绕一根轴的旋转,如果三维空间中的欧拉角旋转要转三次:

上面得到了一个表示旋转的方向余弦矩阵。
不过要想用欧拉角解算姿态,其实我们套用欧拉角微分方程就行了:
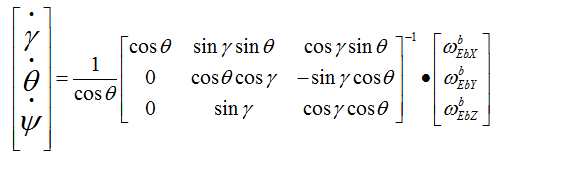
上式中左侧,,是本次更新后的欧拉角,对应row,pit,yaw。右侧,是上个周期测算出来的角度,,,三个角速度由直接安装在四轴飞行器的三轴陀螺仪在这个周期转动的角度,单位为弧度,计算间隔时T陀螺角速度,比如0.02秒0.01弧度/秒=0.0002弧度。间因此求解这个微分方程就能解算出当前的欧拉角。
前面介绍了什么是欧拉角,而且欧拉角微分方程解算姿态关系简单明了,概念直观容易理解,那么我们为什么不用欧拉角来表示旋转而要引入四元数呢?
一方面是因为欧拉角微分方程中包含了大量的三角运算,这给实时解算带来了一定的困难。而且当俯仰角为90度时方程式会出现神奇的“GimbalLock”。所以欧拉角方法只适用于水平姿态变化不大的情况,而不适用于全姿态飞行器的姿态确定。
四元数法只求解四个未知量的线性微分方程组,计算量小,易于操作,是比较实用的工程方法。
我们知道在平面(x,y)中的旋转可以用复数来表示,同样的三维中的旋转可以用单位四元数来描述。我们来定义一个四元数:
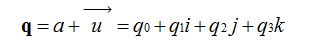
我们可以把它写成,其中,。那么是矢量,表示三维空间中的旋转轴。w是标量,表示旋转角度。那么就是绕轴旋转w度,所以一个四元数可以表示一个完整的旋转。只有单位四元数才可以表示旋转,至于为什么,因为这就是四元数表示旋转的约束条件。
而刚才用欧拉角描述的方向余弦矩阵用四元数描述则为:
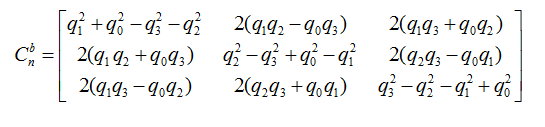
所以在软件解算中,我们要首先把加速度计采集到的值(三维向量)转化为单位向量,即向量除以模,传入参数是陀螺仪x,y,z值和加速度计x,y,z值:
void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az) {
float norm;
float vx, vy, vz;
float ex, ey, ez;
norm = sqrt(ax*ax + ay*ay + az*az);
ax = ax / norm;
ay = ay / norm;
az = az / norm; 下面把四元数换算成方向余弦中的第三行的三个元素。刚好vx,vy,vz 其实就是上一次的欧拉角(四元数)的机体坐标参考系换算出来的重力的单位向量。
// estimated direction of gravity
vx = 2*(q1*q3 - q0*q2);
vy = 2*(q0*q1 + q2*q3);
vz = q0*q0 - q1*q1 - q2*q2 + q3*q3; axyz是机体坐标参照系上,加速度计测出来的重力向量,也就是实际测出来的重力向量。
axyz是测量得到的重力向量,vxyz是陀螺积分后的姿态来推算出的重力向量,它们都是机体坐标参照系上的重力向量。
那它们之间的误差向量,就是陀螺积分后的姿态和加计测出来的姿态之间的误差。
向量间的误差,可以用向量叉积(也叫向量外积、叉乘)来表示,exyz就是两个重力向量的叉积。
这个叉积向量仍旧是位于机体坐标系上的,而陀螺积分误差也是在机体坐标系,而且叉积的大小与陀螺积分误差成正比,正好拿来纠正陀螺。(你可以自己拿东西想象一下)由于陀螺是对机体直接积分,所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。
// integral error scaled integral gain
exInt = exInt + ex*Ki;
eyInt = eyInt + ey*Ki;
ezInt = ezInt + ez*Ki; 用叉积误差来做PI修正陀螺零偏
// integral error scaled integral gain
exInt = exInt + ex*Ki;
eyInt = eyInt + ey*Ki;
ezInt = ezInt + ez*Ki;
// adjusted gyroscope measurements
gx = gx + Kp*ex + exInt;
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt; 四元数微分方程,其中T为测量周期,为陀螺仪角速度,以下都是已知量,这里使用了一阶龙哥库塔求解四元数微分方程:

// integrate quaternion rate and normalise
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT; 最后根据四元数方向余弦阵和欧拉角的转换关系,把四元数转换成欧拉角:

所以有:
Q_ANGLE.Yaw = atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3* q3 + 1)* 57.3; // yaw
Q_ANGLE.Y = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch
Q_ANGLE.X = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // roll
硬件姿态解算
四轴的姿态解算无疑是最繁琐的步骤没有之一,但是自从MPU6050出现了硬件DMP的时候,大妈都能完成姿态解算了!
CrazePony使用了MPU6050自带的硬件四元数单元,可以通过IIC直接读取四元数,省却了软件解算繁琐的算法步骤,非常方便易用。
这里还是要首先介绍下四元数,四元数要说的实在太多,因为它的优点很多,利用起来很方便,但是理解起来就有点蹩脚了。我们百度四元数,一开始看到的
就是四元数来历,还有就是四元数的基本计算。对于来历,还是想说一下,四元数(Quaternions)是由威廉?卢云?哈密尔顿(William
RowanHamilton,1805-1865)在1843 年爱尔兰发现的数学概念。
将实数域扩充到复数域,并用复数来表示平面向量,用复数的加、乘运算表示平面向量的合成、伸缩和旋,这就是我们熟知的复数的二维空间含义,所以人们
会继续猜想,利用三维复数不就可以表达三维空间的变换了吗,历史上有很多数学家试图寻找过三维的复数,但后来证明这样的三维复数是不存在的。有关这个结论
的证明,我没有查到更明确的版本,据《古今数学思想》中的一个理由,三维空间中的伸缩旋转变换需要四个变量来决定:两个变量决定轴的方向,一个变量决定旋
转角度,一个变量决定伸缩比例。这样,只有三个变量的三维复数无法满足这样的要求。但是历史上得到的应该是比这个更强的结论,即使不考虑空间旋转,只从代
数角度来说,三维的复数域作为普通复数域的扩张域是不存在的。并且,据《古今数学思想》叙述,即使像哈密尔顿后来引入四元数那样,牺牲乘法交换律,这样的
三维复数也得不到。经过一些年的努力之后, Hamilton
发现自己被迫应作两个让步,第一个是他的新数包含四个分量,而第二个是他必须牺牲乘法交换律。( 《古今数学思想》第三册177
页)但是四元数用作旋转的作用明显,简化了运算,而且避免了Gimbal Lock,四元数是最简单的超复数,我们不能把四元数简单的理解为3D
空间的矢量,它是4 维空间中的的矢量,也是非常不容易想像的。
我们知道在平面(x,y)中的旋转可以用复数来表示,同样的三维中的旋转可以用单位四元数来描述。我们来定义一个四元数:
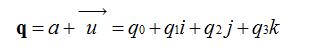
我们可以把它写成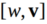 ,其中
,其中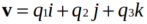 ,
,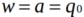 。那么V是矢量,表示三维空间中的旋转轴。w是标量,表示旋转角度。那么
。那么V是矢量,表示三维空间中的旋转轴。w是标量,表示旋转角度。那么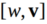
所以大家可以理解为,单位四元数能够表示旋转。我们给出一组单位四元数和欧拉角的转换关系,通过这个关系来将采集到的四元数转化成欧拉角,原理将在软件解算中给出,这里直接使用就可以了:
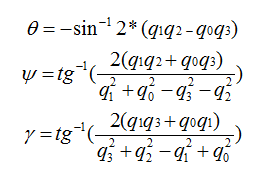
所以在四轴飞行器中,传感器读取到四元数,首先应先将它归一化成单位四元数:
norm = dmpinvSqrt(q[0]*q[0] + q[1]*q[1] + q[2]*q[2] + q[3]*q[3]);
q[0] = q[0] * norm;
q[1] = q[1] * norm;
q[2] = q[2] * norm;
q[3] = q[3] * norm; 归一化后根据四元数和欧拉角转换公式把四元数转化为欧拉角,OK,硬件姿态解算完成!
DMP_DATA.dmp_roll = (atan2(2.0*(q[0]*q[1] + q[2]*q[3]), 1 - 2.0*(q[1]*q[1] + q[2]*q[2])))* 180/M_PI;
// we let safe_asin() handle the singularities near 90/-90 in pitch
DMP_DATA.dmp_pitch = dmpsafe_asin(2.0*(q[0]*q[2] - q[3]*q[1]))* 180/M_PI;
DMP_DATA.dmp_yaw = -atan2(2.0*(q[0]*q[3] + q[1]*q[2]), 1 - 2.0*(q[2]*q[2] + q[3]*q[3]))* 180/M_PI;
四元数
四元数是由爱尔兰数学家威廉?卢云?哈密顿在1843年发现的数学概念。从明确地角度而言,四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话,四元数就代表着一个四维空间,相对于复数为二维空间。
四元数大量用于电脑绘图(及相关的图像分析)上表示三维物件的旋转及方位。四元数亦见于控制论、信号处理、姿态控制、物理和轨道力学,都是用来表示旋转和方位。
相对于另几种旋转表示法(矩阵,欧拉角,轴角),四元数具有某些方面的优势,如速度更快、提供平滑插值、有效避免万向锁问题、存储空间较小等等。
以上部分摘自维基百科-四元数。
姿态解算为什么要用四元数
姿态解算的核心在于旋转,一般旋转有4种表示方式:矩阵表示、欧拉角表示、轴角表示和四元数表示。矩阵表示适合变换向量,欧拉角最直观,轴角表示则
适合几何推导,而在组合旋转方面,四元数表示最佳。因为姿态解算需要频繁组合旋转和用旋转变换向量,所以采用四元数保存组合姿态、辅以矩阵来变换向量的方
案。
总结来说,在crazepony中,姿态解算中使用四元数来保存飞行器的姿态,包括旋转和方位。在获得四元数之后,会将其转化为欧拉角,然后输入到姿态控制算法中。
姿态控制算法的输入参数必须要是欧拉角。AD值是指MPU6050的陀螺仪和加速度值,3个维度的陀螺仪值和3个维度的加速度值,每个值为16位精
度。AD值必须先转化为四元数,然后通过四元数转化为欧拉角。这个四元数可能是软解,主控芯片(STM32)读取到AD值,用软件从AD值算得,也可能是
通过MPU6050中的DMP硬解,主控芯片(STM32)直接读取到四元数。具体参考《MPU60x0的四元数生成方式介绍》。
下面就是四元数软解过程,可以由下面这个框图表示:

四元数的运算
下面介绍一下四元数,然后给出几种旋转表示的转换。这些运算在crazepony的代码中都会遇到。
四元数可以理解为一个实数和一个向量的组合,也可以理解为四维的向量。这里用一个圈表示q是一个四元数(很可能不是规范的表示方式)。
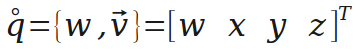
四元数的长度(模)与普通向量相似。
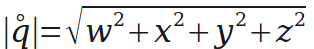
下面是对四元数的单位化,单位化的四元数可以表示一个旋转。
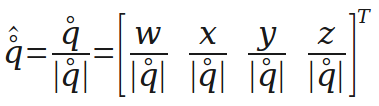
四元数相乘,旋转的组合就靠它了。
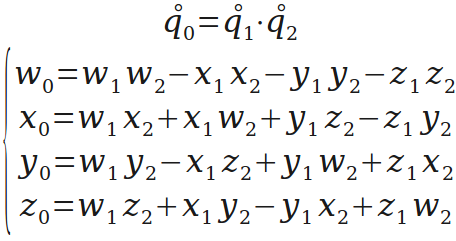
旋转的“轴角表示”转“四元数表示”。这里创造一个运算q(w,θ),用于把绕单位向量w转θ角的旋转表示为四元数。
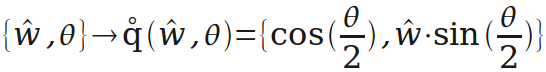
通过q(w,θ),引伸出一个更方便的运算q(f,t)。有时需要把向量f的方向转到向量t的方向,这个运算就是生成表示对应旋转的四元数的(后面会用到)。
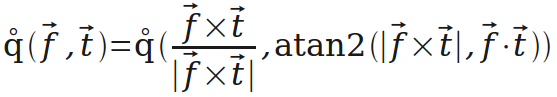
然后是“四元数表示”转“矩阵表示”。再次创造运算,用R(q)表示四元数q对应的矩阵(后面用到)。
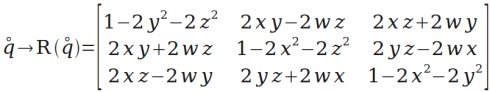
多个旋转的组合可以用四元数的乘法来实现。
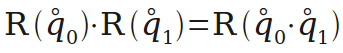
“四元数表示”转“欧拉角表示”。用于显示。

陀螺仪
陀螺仪,测量角速度,具有高动态特性,但是它是一个间接测量角度的器件,它测量的是角度的导数,角速度,要将角速度对时间积分才能得到角度。
如果这个世界是理想的,美好的,那我们的问题到此就解决了,不过很遗憾,现实是残酷的,误差的引入,使得积分出现了问题。
假设陀螺仪固定不动,理想角速度值是0dps(degree per
second),但是有一个偏置0.1dps加在上面,于是测量出来是0.1dps,积分一秒之后,得到的角度是0.1度,1分钟之后是6度,还能忍受,
一小时之后是360度,转了一圈,也就是说,陀螺仪在短时间内有很大的参考价值。
陀螺仪就是内部有一个陀螺,它的轴由于陀螺效应始终与初始方向平行,这样就可以通过与初始方向的偏差计算出实际方向。传感器MPU6050实际上是
一个结构非常精密的芯片,内部包含超微小的陀螺。陀螺仪运转一段时间以后,noise和offset会导致数据偏差,需要借助其它传感器进行较正。
使用陀螺仪获得角度,一定要考虑积分误差的问题。
加速度计
加速度计可以测量加速度,包括重力加速度,于是在静止或匀速运动的时候,加速度计仅仅测量的是重力加速度,而重力加速度与刚才所说的R坐标系是固连的,通过这种关系,可以得到加速度计所在平面 与 地面 的角度关系.
但是加速度计若是绕着重力加速度的轴转动,则测量值不会改变,也就是说无法感知这种水平旋转。
关于MPU6050
MPU-60×0是全球首例9轴运动处理传感器。它集成了3轴MEMS陀螺仪,3轴MEMS加速度计,以及一个可扩展的数字运动处理器
DMP(Digital Motion
Processor),可用I2C接口连接一个第三方的数字传感器,比如磁力计。扩展之后就可以通过其I2C或SPI接口输出一个9轴的信号(SPI接口
仅在MPU-6000可用)。MPU-60×0也可以通过其I2C接口连接非惯性的数字传感器,比如压力传感器。
MPU-60×0对陀螺仪和加速度计分别用了三个16位的ADC,将其测量的模拟量转化为可输出的数字量。为了精确跟踪快速和慢速的运动,传感器的
测量范围都是用户可控的,陀螺仪可测范围为±250,±500,±1000,±2000°/秒(dps),加速度计可测范围
为±2,±4,±8,±16g。一个片上1024
字节的FIFO,有助于降低系统功耗。和所有设备寄存器之间的通信采用400kHz的I2C接口或1MHz
的SPI接口(SPI仅MPU-6000可用)。对于需要高速传输的应用,对寄存器的读取和中断可用20MHz的SPI。另外,片上还内嵌了一个温度传感
器和在工作环境下仅有±1%变动的振荡器。
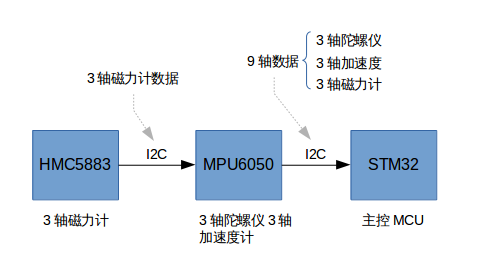
在crazepony上,MPU6050,HMC5883传感器之间的连接如下图所示。
MPU6050中DMP应用
在Crazepony-II上,测试了软件解算四元素,然后通过四元素解算姿态角这种实现方式,其实总的来说,并没感觉36MHz的主控压力有多大,没有出现机身不稳,卡死的情况。

同时,本着务实他的态度,我们也测试了MPU6050的硬解四元素,即从IIC总线上读到的数据不再是MPU60x0的AD值,而是通过初始化对
DMP引擎的配置,从IIC总线上读到的直接就是四元素的值,从而跳过了程序通过AD值计算四元素这个看起来繁琐的步骤。测试结果是,机身反应的确要比之
前反应灵活,最关键的一点是,这样得出的偏航角(Yaw)很稳很稳,基本不会漂移或者说漂移小到了可以容忍的地步。
最后,MPU60x0的强大之处不仅于此,它支持一个从IIC接口,可以外部接上一个磁力计,如HMC5883,这样一来,DMP引擎可以直接输出
一个绝对的方向姿态,即能够输出一个带东西南北的姿态数据包,很厉害的样子。在Crazepony-II第四版将会加上这样一个磁力计,相信它再也不会迷
路了~~

转载自:http://www.crazepony.com/book/




